binarized_network

Deep neural networks often suffer from over-parametrization and large amounts of redundancy in their models. Which call for many resources (processing power, memory, battery time, etc), and sometimes critically constrained in applications running on embedded devices.
Training such a deep neural networks was also computational demanding and time consuming. Thus recently many model compression methods were proposed, an extreme method is called the binarized network.

Straight Through Estimator

When quantization the network weights and activations with binary values, the biggest problem is the gradient back-propagation, cause the gradient of the binarization function is always zero. To overcome this, Straight Through Estimator was introduced by Hinton$_{[1]}$ & Bengio$_{[2]}$.

Straight-Through Estimator:The idea is simply to back-propagate through the hard threshold function (1 if the argument is positive, 0 otherwise) as if it had been the identity function.

Binarization Functions

Many binarization functions were proposed till now, mainly based on the $\mathbf{Sign}$ function:

• Stochastically Binarization

  • $P(w^b = +1) = \frac{w + 1}{2}, P(w^b = -1) = 1 - P(w^b = +1)$,
    where $w$ was scaled to $[-1, 1]$ $_{[5]}$ or the probability was restricted to $[0, 1]$ $_{[4]}$.

• Deterministic Binarization

  • $w^b = \mathbf{Sign}(w)$,
    with$_{[6]}$ or without$_{[3],[7]}$ a scaling factor $\alpha$.

Recent works

Bitwise Neural Networks$_{[3]}$

The author proposed a two-staged approach:

1. A typical network training with a weight compression technique which help the real-valued model to be easily converted into BNN.
   • The weights were compressed by $tanh$, which wrap the weights to have value between -1 and +1.
   • Similarly, $tanh$ is also chosen for the activation.
2. Use the compressed weights to initialize the BNN parameters and do noisy back-propagation based on the tentative bitwise parameters.
   • A sparsity parameter $\lambda$ was introduced to decide the proportion of zeros after binarization, which decide a boundary $\beta$, and the weights were divided into three group $\{-1, 0, 1\}$:
     • $w_{i,j} = -1$, if $w_{i,j} < -\beta$
     • $w_{i,j} = +0$, if $|w_{i,j}| < \beta$
     • $w_{i,j} = +1$, if $w_{i,j} > \beta$
   • The weights were updated with real-values parameters during the back-propagation progress.

Thus, in the feed-forward only XNOR and bit-counting operations are used instead of multiplication, addition, and non-linear activation on floating or fixed-point variables.

BinaryConnect Github$_{[4]}$

In this work, only the weights are binarized, and the weights are only binarized during the forward and backward propagation but not during the parameter update.

• The real-valued weights are clipped within $[-1, 1]$
• Batch Norm and Adam are used.
• The BinaryConnect are proved to act as regularizer.

1. SGD explores the space of parameters by making small and noisy steps and that noise is averaged out by the stochastic gradient contributions accumulated in each weight. Therefore, it is important to keep sufficient resolution for these accumulators, which at first sight suggests that high precision is absolutely required.

2. Noisy weights actually provide a form of regularization which can help to generalize better. And previous works showed that only the expected value of the weight needs to have high precision, and that noise can actually be beneficial.

Neural Networks with Few Multiplications$_{[5]}$

The author proposed a two-staged method:

1. Stochastically binarize weights to convert multiplications involved in computing hidden states to sign changes.
   • The weights are forced to be a real value in the interval $[-1, 1]$.
2. Quantize the representations at each layer to convert the remaining multiplications into binary shifts while back-propagating error derivatives (called quantized back propagation).
   • The activations $x$ in back-propagation computation are quantized to be integer power of 2 to convert the multiplications into binary shifts.

A somewhat surprising fact is that instead of damaging prediction accuracy the approach tends improve it, which is probably due to several facts.

First is the regularization effect that the stochastic sampling process entails.

The second fact is low precision weight values. Low precision prevents the optimizer from finding solutions that require a lot of precision, which more likely correspond to overfitted solutions.

XNOR-Net Github$_{[6]}$

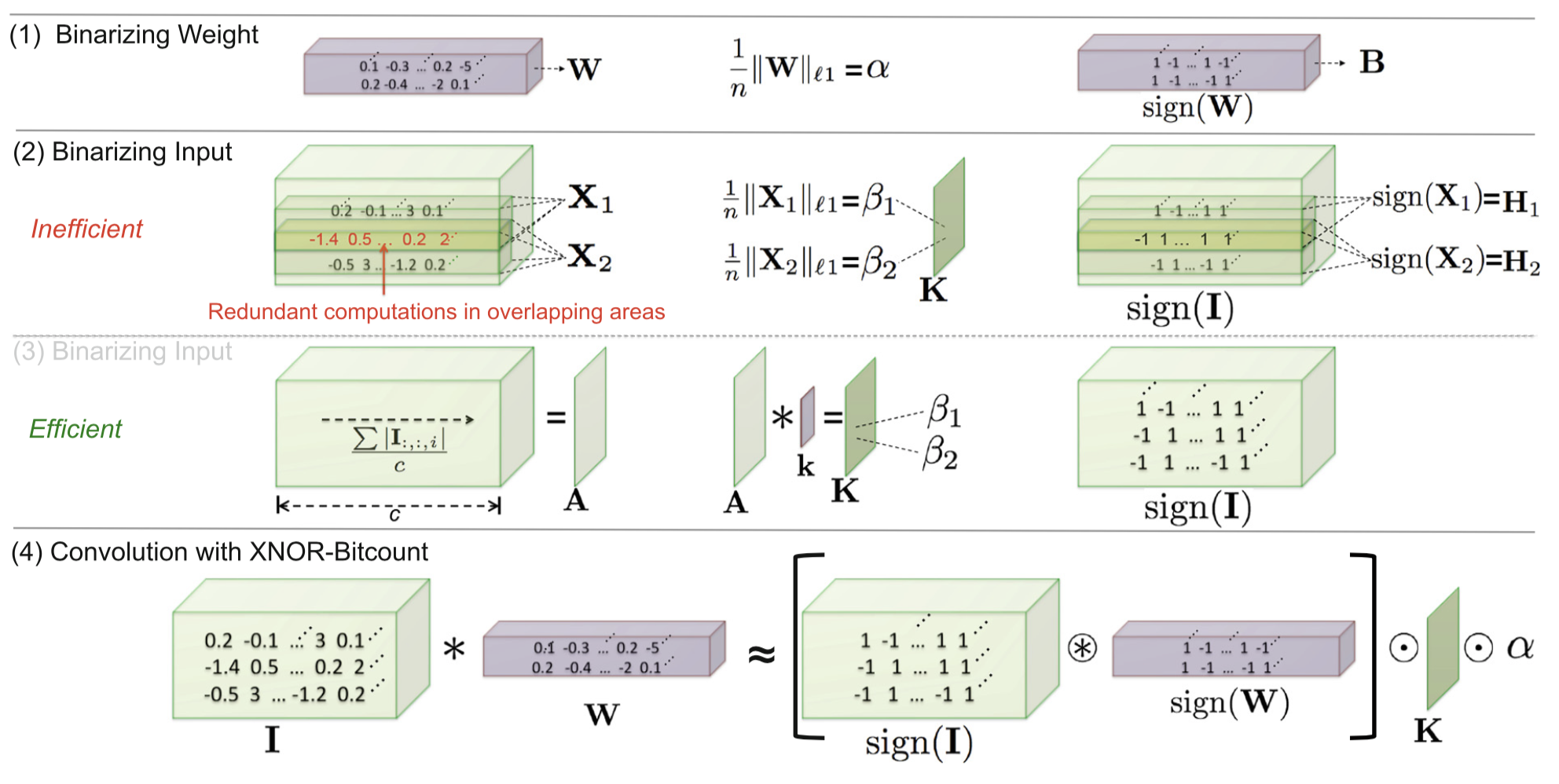
The author introduced a new way to binarize the weights and activations, and introduce a XOR-net which.

Estimate the real-value weight filter $W$ using a binary filter B \in \{+1, −1\}^{c×w×h} and a scaling factor \alpha ∈ R^+ such that $W \approx \alpha B$. Then a convolutional operation can be approximated by \mathbf{I * W ≈ (I \bigoplus B)} \alpha.

1. The new binarization method is to solve the optimization function:
   J(\mathbf{B},\alpha) = \|\mathbf{W} − \alpha \mathbf{B}\|2
   $\alpha^*,\mathbf{B}^* = \mathbf{argmin}\{\alpha, \mathbf{B}\} \mathbf{J(B},\alpha)$
   With the optimal solution of $\mathbf{B}$ and $\alpha$:
   • $B^* = \mathbf{sign(W)}$
   • $\alpha^* = \frac{\mathbf{W^T B^*}}{n} = \frac{\mathbf{W^T sign(W)}}{n} = \frac{\sum|\mathbf{W}_i|}{n} = \frac{1}{n} \|\mathbf{W}\|_{\ell1}$
   • Calculate gradient of $\mathbf{sign(r)}$ as Binarized neural network: which has $\frac{\partial{sign}}{\partial{r}} = r 1_{|r| \leq 1}$
2. To further binarize the activation, similar to the previous method, the dot product between $\mathbf{X, W \in R^n}$ is approximated by $\mathbf{X^TW} \approx \beta\mathbf{H^T}\alpha\mathbf{B}$, where \mathbf{H, B} \in \{+1, −1\}^n and $\beta, \alpha \in \mathbf{R}^+$. By define $\mathbf{Y} \in \mathbf{R}^n$ such that $\mathbf{Y}_i = \mathbf{X}_i\mathbf{W}_i$, \mathbf{C} \in \{+1,−1\}^n such that $\mathbf{C}_i = \mathbf{H}_i\mathbf{B}_i$ and $\gamma \in \mathbf{R}^+$ such that $\gamma = \beta\alpha$. Also the optimal solution are solved:
   • $C^* = \mathbf{sign(Y)} = \mathbf{sign(X)} \odot \mathbf{sign(W)} = \mathbf{H}^* \odot \mathbf{B}^*$
   • $\gamma^* = \frac{\sum|\mathbf{Y}_i|}{n} = \frac{\sum|\mathbf{X}_i||\mathbf{W}_i|}{n} \approx (\frac{1}{n} \|\mathbf{X}\|_{\ell1}) (\frac{1}{n} \|\mathbf{W}\|_{\ell1}) = \beta^*\alpha^*$
3. By average across the channel first and get $\mathbf{K}$ which contain scaling factors $\beta$ for all sub-tensors in the input $\mathbf{I}$. We have:
   • $\mathbf{I} * \mathbf{W} \approx (\mathbf{sign(I)} \otimes \mathbf{sign(W)}) \odot \mathbf{K} \alpha$
     
4. To decrease the information loss during the binarization, the structure of convolution block is changed to:
   

The key difference of our method is using a scaling-factor, which does not change the order of efficiency while providing a significant improvement in accuracy.

Binarized neural networks Github$_{[7]}$

This work is an extension of $_{[4]}$, and also published as $_{[8],[9]}$.

• The gradient was calculated using the straight through estimator $\frac{\partial{sign}}{\partial{r}} = r 1_{|r| \leq 1}$, which preserves the gradient’s information and cancels the gradient when r is too large.
• The weights are constrained to real-value between $[-1, 1]$, and $\mathbf{Sign}$ function is used to binarize the activations and weights.
• Shifted based version of BatchNorm and Adam were introduced for speeding up computation.

Our method of training BNNs can be seen as a variant of Dropout, in which instead of randomly setting half of the activations to zero when computing the parameter gradients, we binarize both the activations and the weights.

DoReFa-Net$_{[10]}$

The author extend the definition of Straight Through Estimator and proposed several STEs, one to quantize the activation with k-bit number, and the other is the k-bit extended version of the STE used in XNOR-net.

• The weights are limited in the range of $[-1, 1]$ by $tanh$.
• Not only the activations and the weights, the gradients are also quantized with k-bit number.

We find that weights and activations can be deterministically quantized while gradients need to be stochastically quantized.

Reference

[1]. Hinton, G. Neural networks for machine learning. Coursera, video lectures, 2012.
[2]. Y. Bengio, N. Léonard, and A. Courville, “Estimating or Propagating Gradients Through Stochastic Neurons for Conditional Computation,” arXiv.org, vol. cs.LG. p. arXiv:1308.3432, 15-Sep-2013.
[3]. M. Kim and P. Smaragdis, “Bitwise Neural Networks,” presented at the International Conference on Machine Learning, 2015, pp. 1–5.
[4]. M. Courbariaux, Y. Bengio, and J.-P. David, “BinaryConnect: Training Deep Neural Networks with binary weights during propagations,” presented at the Advances in Neural Information Processing Systems, 2015, pp. 1–9.
[5]. Z. Lin, M. Courbariaux, R. Memisevic, and Y. Bengio, “Neural Networks with Few Multiplications,” presented at the International Conference on Learning Representations, 2016, pp. 1–9.
[6]. M. Rastegari, V. Ordonez, J. Redmon, and A. Farhadi, “XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks,” presented at the European conference on computer vision, Amsterdam, The Netherlands, 2016, pp. 525–542.
[7]. I. Hubara, M. Courbariaux, D. Soudry, R. El-Yaniv, and Y. Bengio, “Binarized neural networks,” presented at the Advances in Neural Information Processing Systems, 2016, pp. 4114–4122.
[8]. M. Courbariaux, I. Hubara, D. Soudry, R. El-Yaniv, and Y. Bengio, “Binarized Neural Networks: Training Neural Networks with Weights and Activations Constrained to +1 or −1,” arXiv.org, vol. cs.LG. p. arXiv:1602.0283, 17-Mar-2016.
[9]. I. Hubara, M. Courbariaux, D. Soudry, R. El-Yaniv, and Y. Bengio, “Quantized Neural Networks: Training Neural Networks with Low Precision Weights and Activations.,” arXiv.org, vol. cs.NE. p. arXiv:1609.07061, 22-Sep-2016.
[10]. S. Zhou, Y. Wu, Z. Ni, X. Zhou, H. Wen, and Y. Zou, “DoReFa-Net: Training Low Bitwidth Convolutional Neural Networks with Low Bitwidth Gradients,” arXiv.org, vol. cs.NE. p. arXiv:1606.06160, 02-Feb-2018.